Методика математического развития детей дошкольного возраста: тренируем левое полушарие

Дошкольный возраст – это время, когда познавательное, нравственное, физическое развитие ребенка происходит особенно интенсивно. В частности, именно до 5-6 лет ребенок приобретает более половины суммарных навыков мышления, которые пригодятся ему в будущем. Именно поэтому ему необходимо уделять особое внимание. В частности именно в этом возрасте у ребенка должны отложиться первые математические навыки. Рассмотрим теоретические основы математического развития детей младшего и старшего дошкольного возраста.

Занятие по математике в детсаду, старшая группа

Почему это так важно?

1. Математика является одним из наиболее значимых, предметов.

   Однако именно он зачастую вызывает у учащихся немалые трудности

2. Изучение этого предмета благотворно сказывается на познавательных способностях ребенка (мышлении, памяти, речи)
3. Математические навыки совершенствуют эмоционально-волевую сферу, формируют настойчивость и целеустремленность
4. Совершенствуется основы воображения ребенка

Роль математики в жизни

К окончанию дошкольного периода ребенок должен обладать следующими математическими умениями и навыками:

• Способность к сравнению величин по базовым признакам; сформированность представлений о понятиях «больше-меньше», «выше-ниже» и т.д.
• Способность к группировке предметов по их базовым свойствам (основы — величина, цвет, назначение, материал, форма)
• Способность к сопоставлению части-целого; умение собирать картинку не менее чем из 12-24 фрагментов
• Сформированные навыки счета и умение производить математические операции с числами в пределах десяти
• Сформированность у детей количественных и качественных представлений предмета

Суть математического развития

Необходимые условия проведения математических занятий с ребенком

На чем строится теория и методика математического развития для дошкольников? Для того чтобы занятия были по-настоящему интересны для ребенка, а информация усваивалась им быстрее и легче, их необходимо строить с учетом следующих рекомендаций:

1. Использование наглядного дидактического материала, подобранного с учетом возрастных и других индивидуальных особенностей ребенка
2. Наличие у занятия четкого сюжета, согласно которого будет происходить его развитие
3. Подбор задач в строгом соответствии с возрастными особенностями ребёнка, уровнем его интеллектуального развития
4. Использование разнообразных методов и форм для создания основы работы (к ним можно отнести решение логических задач, дидактические игры, работа с раздаточным материалом и т.д.)
5. Многозадачность (направленность на развитие пространственных, временных, количественных представлений)
6. Использование игровой формы ведения занятий
7. Акцент на формировании игровой мотивации; элементы сюрпризов и внезапности
8. Помощь ребенку не только в освоении определенной системы знаний и навыков, но также развитие у него навыков самостоятельной познавательной активности, независимости суждений и т.д.
9. Формирование оптимальной развивающей среды для развития у ребенка базовых познавательных процессов
10. Научение детей восприятию количественных и качественных особенностей предмеов, формирование соответствующих представлений

Задачи развития математических способностей

Особенности формирования математических представлений в зависимости от возраста

Учитывая то, что дошкольный возраст условно подразделяется на три основных периода, цели, задачи, а также методы и формы математического воспитания детей также будут различаться.

Младший дошкольный период. В это время необходимые математические навыки и представления только начинают развиваться. Поэтому ребенку необходимо дать представление о базовых операциях.

Лучшими играми на развитие навыков мышления – детская мозаика (от 5 фрагментов), сложение геометрических фигур (от 4 деталей).

Средний дошкольный период. Происходит активное развитие знаково-символической функции сознания. Ребенка уже можно приучать к счету и самым простым математическим операциям. Закладываются основы логического мышления.

К числу наиболее предпочтительных игр относятся: «Нелепицы», «Сосчитай предметы, «Найди пару», «Математическое лото», «Домино фигур».

Для развития аналитико-синтетических способностей ребенка ему можно предложить игры наподобие танграма, где ему нужно будет составить из отдельных частей геометрическую фигуру, силуэт животного и т.д.

Индивидуальное занятие на определение уровня математического развития

В старшем дошкольном возрасте для детей все более заметную и значимую роль начинает играть самостоятельность ребенка, его способность к самоорганизации. Все более значимую роль приобретает логическое мышление.

Ребёнок начинает пробовать составлять рассказы по картинкам, составлять логические ряды, соблюдая правильную последовательность элементов.

Математические тесты для малышей 3-4 лет

Какие методы лучше всего использовать для развития математических представлений дошкольника?

Наглядный метод играет наиболее важную роль в обучении детей математике, особенно – если речь идет о младшем дошкольном периоде.

Методы развития математических знаний

Различают следующие разновидности наглядного метода обучения:

• Работа с раздаточным, либо демонстрационным материалом. Использование бессюжетного или сюжетного метода (за основу можно взять сюжет любой знакомой ребенку сказки, где фигурировали бы счет или числа)
• Объемный или плоскостной. Занятия с использованием специальных счетных материалов (например, детских счет, палочек, кубиков и т.д.)
• Самодельный, либо фабричный.

Раздаточный материал для математических занятий

Для того чтобы эффективнее использовать наглядный материал, необходимо строить развивающие занятия с учетом следующих закономерностей:

1. Изучение каждой новой темы должно начинаться с более объемного наглядного материала. Это упростит его восприятие ребенком
2. По мере взросления ребенка необходимо сделать так, чтобы доля объемного и сюжетного наглядного материала понижалась, а доля плоского и бессюжетного возрастала
3. Желательно использовать несколько типов наглядного материала для решения одной программной задачи
4. Очень желательно заранее ознакомить ребенка с новым для него для него материалом

Отдельно стоит рассмотреть требования, предъявляемые к наглядным пособиям.

Дидактический материал для занятий

Как мы уже указали выше, он может быть как готовым заводским, так и сделанным руками родителей. Тем не менее важно, чтобы он соответствовал следующему:

• Гигиеничность. Игрушки должны быть сделаны из экологически чистых, безопасных материалов и иметь все необходимые сертификаты
• Эстетичность. Привлекательный материал скорее привлечет внимание ребенка
• Реальность, позволяющая ребенку воспринимать изучаемый материал без искажений
• Прочность и надежность
• Разнообразие и достаточное количество для возможности использовать вариативные техники
• Принцип логического построения, объединяющего основы материала
• Однородность

Игровой уголок с дидактическим материалов

Существенным плюсом практического метода обучения является то, что он в наиболее полной степени объясняет ребенку то, зачем он изучает тот или иной материал. И как именно полученные знания смогут пригодиться ему в будущем?

1. Активное применение на практике разнообразного дидактического материала
2. Выполнение разнообразных как умственных, так и практических действий
3. Развитие навыка прогнозирования результата действий с дидактическим материалом различного вида
4. Не только привитие ребенку математических навыков, но и подробное разъяснение их роли в жизни ребенка (в игровой деятельности, в быту и т.д.)

• Словесный метод обучения строится на непосредственном взаимодействии ребенка с родителем, либо воспитателем.
• Именно поэтому основные требования, предъявляемые к этому методу, будут направлены на речь участников процесса
• Речь родителя, либо воспитателя, должна быть:

• Грамотной
• Четкой
• Эмоциональной и живой
• Доступной
• Доброжелательной
• Умеренно громкой

Развитие речи на занятиях по математике

Темп речь, ее интонацию и другие особенности необходимо корректировать в зависимости от индивидуально-возрастных особенностей ребенка. Например, ребенок младшего дошкольного возраста намного лучше воспринимает довольно медленную речь; несформированные процессы памяти требуют многократных повторений.

Развитие логики и пространственного мышления в игровой форме

Разговаривая с ребенком более старшего возраста, можно несколько ускорить темп речи, а также активнее использовать проблемные ситуации.

Определенные требования предъявляются также и к речи детей. Она должна быть:

• Грамотная
• Содержать необходимую математическую терминологию и основы математики по возрасту
• Разборчивая и понятная
• Ребенок должен говорить полными распространенными предложениями с правильным грамматическим строем
• Иметь достаточную громкость

Структура математического занятия для дошкольника

Правильная структура занятия является еще одним важным условием, на котором строится методика математического развития детей дошкольников.

Используемые игры на занятиях по математике

1. Вводная часть. Логическая разминка. Включает в себя наиболее простые задания для детей, которые должны «разогреть» ум ребенка, заинтересовав его и подготовив к занятию
2. Основная часть занятия, в ходе которой происходит изучение нового материала для формирования математических представлений, либо закрепление уже изученного. Упражнения можно подбирать при помощи специальной методической литературы (хорошим примером может стать книга, которую составила Щербакова Е.И. «Теория и методика математического развития для дошкольников»).
3. 3Пальчиковая гимнастика. Переключает внимание ребенка, служит предупреждением переутомления. Для этих же целей можно использовать физминутку (если занятие было связано преимущественно с интеллектуальной деятельностью), артикуляционную гимнастику или упражнения для глаз (если у ребенка было активное занятие с использованием подвижных игр).
4. Повторение пройденного материала.
5. Рисование, шнуровка, либо игры, направленные на развитие мелкой моторики.

Изучение формы и размера на занятиях физкультуры

Развитые математические навыки у детей дошкольного возраста позволит ему не только успешно приступить к школьному обучению, но и сформировать у себя такие качества, как усидчивость, внимание, целеустремленность.

Источник: https://detki.guru/razvitie-rebenka/teoriya-i-metodika-matematicheskogo-razvitiya.html

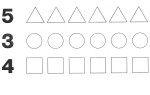
Методика математического развития детей дошкольного возраста как наука

СВЯЗЬ С ДРУГИМИ НАУКАМИ Подготовка детей к усвоению математики в школе не может успешно осуществляться без связи с методикой начального обучения математике и некоторыми аспектами самой математики, которые служат теоретической основой обучения дошкольников и младших школьников. Опора на эти науки позволяет определить объем и содержание математических знаний, которые должны быть освоены ребенком в детском саду и служить фундаментом математического образования.

СВЯЗЬ С ДРУГИМИ НАУКАМИ Наиболее важными являются такие фундаментальные математические понятия, как «множество» , «отношение» , «число» , «величина» . Совершенствование содержания и методов обучения математике в школе предполагает новое отношение к подготовке детей в детском саду.

В настоящее время внесены существенные изменения в содержание математической подготовки дошкольников; найдены и апробированы более эффективные методы и средства обучения.

Связь с методикой обучения математике в начальной школе позволяет верно определять основные пути дальнейшего совершенствования методики математического развития дошкольников.

СВЯЗЬ С ДРУГИМИ НАУКАМИ Философия, особенно ее составляющая – теория познания, разрабатывает методы познания, которые используются в методических исследованиях и в реальном процессе обучения математике. Например, системный подход широко используется в исследованиях методического характера.

Диалектический подход к исследованию методических проблем позволяет точно расставить акценты в их решении. Так, с помощью диалектического метода устанавливаются соотношения между целями и содержанием математического образования.

Деятельностная концепция знаний помогает решать проблемы, связанные с формированием математических представлений, решением задач.

СВЯЗЬ С ДРУГИМИ НАУКАМИ Также методика математического развития дошкольников тесно связана с психологией. Так, для обоснованного отбора материала необходимо использовать закономерности развития познавательной деятельности, памяти, восприятия, мышления, внимания детей той или иной возрастной группы.

На выбор приемов, системы упражнений и на последовательность органи зации деятельности детей в процессе усвоения математического материала большое влияние оказывает общепризнанная теория поэтапного формирования умственных действий (П. Я. Гальперин, Н. Ф. Талызина).

Психология также определяет возрастные возможности детей в усвоении знаний и умений, которые не являются чем то застывшим и меняются в зависимо сти от типа обучения.

Закономерности протекания физиологических процессов у дошкольников служат основой для определения места и длительности непосредственно образовательной деятельности по формированию математических представлений для каждой возрастной группы детского сада, обусловливают саму их структуру, сочетание и чередование различных методов и средств обучения, разных по характеру видов деятельности (включение физминуток, дозирование учебно познавательных задач и т. д. ).

РОЛЬ ОБУЧЕНИЯ МАТЕМАТИКЕ ДЛЯ РАЗВИТИЯ ЛИЧНОСТИ РЕБЕНКА Умственное (восприятие , речь, внимание, память, сенсорика, мышление, матем. ЗУН и др.

) Трудовое (математика является тяжелым трудом) Физическое (развитие мускулатуры кистей рук, спины, глаз) Нравственное (дисциплинированность, организованность, ответственность, аккуратность) Эстетическое (красота математической мысли, эстетика пособий, чертежей, моделей)

«СОВРЕМЕННЫЕ ТЕХНОЛОГИИ МАТЕМАТИЧЕСКОГО ОБРАЗОВАНИЯ ДОШКОЛЬНИКОВ» КАК УЧЕБНЫЙ ПРЕДМЕТ Под учебным предметом понимается дидактически обоснованная система знаний, умений и навыков, отражающая основное содержание той или иной науки.

Учебный предмет «Современные технологии математического образования дошкольников» направлен на раскрытие дидактически обоснованной системы знаний, умений и навыков, отражающих основное содержание такой науки как методика математического развития дошкольников.

ОСНОВОПОЛАГАЮЩИЕ ИДЕИ 1. Научное понимание процесса обучения как активной деятельности, направленной на интеллектуальное, в частности математическое, развитие личности ребенка. 2.

Переход от репродуктивного типа обучения на продуктивный, развивающий, творческий, предусматривающий перестройку всей системы учебно воспитательной работы в детском саду с учетом интересов и познавательных возможностей каждого ребенка. 3.

Вариативность программ и методических обоснований предполагает дифференциацию и индивидуализацию обучения, гарантирует обеспечение государственных стандартов образования и достаточно высокий уровень развития детей.

ПРЕДМЕТ ДАННОЙ УЧЕБНОЙ ДИСЦИПЛИНЫ направляемый взрослым процесс освоения ребенком математического содержания, способствующего познавательному, личностному развитию при условии специальной организации и применения в обучении эффективных методов, форм и средств развития и воспитания. Содержание, методы и приемы, формы и средства обучения обусловлены основными закономерностями освоения детьми способов познания, простых математических связей и зависимостей, преемственностью в математическом развитии детей дошкольного и младшего школьного возраста

ЗАДАЧИ ДАННОЙ УЧЕБНОЙ ДИСЦИПЛИНЫ ознакомление студентов с некоторыми вопросами теории элементарной математики, особенностями детских представлений о количестве, величине, форме, пространстве и времени, с методами и организационными формами обучения детей математике в разных возрастных группах детского сада в соотнесении с требованиями дидактики, развитие личностных качеств студентов, познавательных способностей, формирование у них ключевых компетенций.

СПАСИБО ЗА ВНИМАНИЕ

Источник: https://present5.com/metodika-matematicheskogo-razvitiya-detej-doshkolnogo-vozrasta-kak-nauka/

Диагностика математического развития детей дошкольного возраста

В процессе развития и воспитания детей дошкольного возраста особое значение имеет педагогическая диагностика. Данный процесс является актуальной задачей, которая направлена на определение правильности образовательных действий. При этом диагностика выполняет, также, и другие функции, но, в любом случае, является необходимым процессом, как для старших дошкольников, так и детей школьного возраста. Диагностический метод работы на определение математического развития представляет собой один из основных процессов, который имеет некоторые особенности.

Цель диагностики

Диагностика математического развития детей в период дошкольного возраста является важным процессом, который направлен на получение информации о тенденции изменения и состоянии объекта. Полученные данные используются для коррекции процесса обучения, выявления новых направлений и обеспечения необходимого уровня педагогических действий. Такой метод является не только важным, но и необходимым для комплексного и целенаправленного развития ребенка дошкольного и старшего возраста.

Диагностика выполняет следующие функции:

• Оптимизация индивидуального процесса обучения;
• Обеспечение правильного определения результатов педагогических действий и методов;
• Минимизация ошибок при оценке уровня знаний ребенка;
• Определение правильности направления деятельности педагога.

Цели, которые преследует диагностика математических представлений, являются неотъемлемой частью качественного процесса обучения. Если отсутствует данный этап работы, то эффективность развивающих занятий определить достаточно сложно. При этом также невозможно знать правильность направления педагогической деятельности и качество знаний ребенка.

Занятия для физического развития ребенка имеют особое значение, но существенную роль также играют методики, направленные на развитие логики, умственных способностей. Диагностика позволяет узнать уровень математических навыков.

Такие способности определяют логическое мышление и требуют постепенного развития. Обусловлено это тем, что у человека на момент рождения левое полушарие головного мозга развито достаточно слабо, а ведь именно оно отвечает за процесс логического мышления.

Последующий процесс обучения и приобретения навыков развивает данную область, интеллект и умственные способности.

Перед началом обучения лучше всего провести диагностический процесс, что позволит определить исходные навыки и уровень развития ребенка. После этого подбираются оптимальные методы работы, которые позволяют решить те или иные задачи. Основные признаки обследования для детей дошкольного и старшего возраста заключаются в следующем:

• Определенная цель и задача оценки состояния объекта;
• Систематичность процесса диагностирования как вида работы педагога;
• Применение методов, которые специально предназначены для данной работы или адаптированы для диагностики;
• Доступность данного вида деятельности для осуществления педагогами.

Существуют различные методики, которые направлены на определение состояния диагностируемого объекта. Данный процесс предполагает преемственность и последовательность, а также доступность методики для педагога.

В данном случае могут использоваться различные технологии работы, например, наглядные варианты занятий в виде тестов с картинками. Определенный тип диагностики подбирается в зависимости от степени развития детей.

Особенности диагностики

Детям 4 — 6 лет важно обеспечить комфортное знакомство с математическими понятиями, что обеспечит правильное восприятие информации. Различные методики используются для подготовки к школе, позволяя в дальнейшем получить высокий результат обучения. В данном случае педагог подбирает оптимальные варианты работы, программы, пособия и материалы. Все средства обучения должны соответствовать необходимым стандартам, а определить правильность действий поможет диагностика математического развития детей.

Знакомство с математическими понятиями, действиями и другими процессами предполагает решение таких задач как:

• Знание отличительных черт понятий «цифра» и «число»;
• Количественный и порядковый счет;
• Сложение и вычитание в пределах десятка;
• Знания о форме и объеме предметов;
• Измерение высоты, длины и ширины предметов;

Ориентирование в пространстве, учитывая такие понятия как «ближе», «дальше», «впереди» и др.

Освоение данной информации для детей дошкольного и старшего возраста является важным моментом. Поэтому в деятельности педагога должны использоваться различные методики, которые направлены на логическое, умственное развитие мышления. В каждом случае требуется диагностика развития математического мышления у ребенка.

Формирование математических представлений у детей — это процесс, который может осуществляться как в домашних условиях, так и в дошкольных образовательных учреждениях.

Профессиональные педагоги чаще всего проводят общие занятия в группах, которые также могут иметь игровую форму. При этом развиваются коммуникативные навыки и организованность действий.

Помимо физического развития важно уделять существенное внимание логической деятельности. Для этой цели существует множество различных методик, например, игры, тесты или задачи на сравнение.

Например, эффективным методом является подсчет предметов вслух или наглядное объяснение принципов вычитания, а также сложения.

Такой подход облегчит ребенку решение задач в начальной школе и обеспечит хороший уровень подготовки.

Для формирования у ребенка представлений математического типа важно освоить несколько умений.

Профессиональный педагог чаще всего использует для работы специальный детский набор, который включает в себя геометрические фигуры, счетные палочки и другие элементы.

Такой многофункциональный комплект облегчает ребенку усвоение новой информации, так как решение задач происходит на наглядном примере.

Ребенок может создавать различные группы из фигур, освоить геометрические формы, например, квадрат или треугольник. В любом случае важно структурировать методики обучения и обеспечить комфортную подачу информации.

Логическое мышление и диагностика

Математическое мышление тесно связано с логической деятельностью. Именно поэтому для детей дошкольного возраста важно осуществлять комплексное, оптимальное и эффективное применение специальных методик. Процесс образования включает в себя проведение операций над определенными объектами. Например, нахождение отличий или сходства двух предметов, группировка деталей по необходимому признаку. На основе подобных задач осуществляется развитие логической деятельности у ребенка.

Данный вид методики позволяет гораздо более успешно решать задачи в период обучения в школе и более эффективно усваивать новую информацию.

Профессиональный педагог определяет необходимый тип работы, методики и осуществляет диагностику. В данном случае является важным переход педагога от обучающего на уровень диагностирующего. В результате этого происходит и смена деятельности, создается диагностическая ситуация для определения математического развития детей в дошкольный период.

Каждая диагностическая ситуация требует особенного подхода. Данный процесс представляет собой взаимодействие педагога и ребенка. При этом дети должны быть активно вовлечены в процесс, отражая результат своей логической деятельности. Таким образом, в дошкольном периоде осуществляется тщательная подготовка к школе, и ребенок получает необходимые базовые знания.

Процесс диагностики заключается в использовании различных методик, подобранных в соответствии с целью, особенностями развития ребенка и возраста детей.

В результате наблюдения, применения необходимых материалов и пособий можно получить полную информацию о степени развития объекта.

Полученные данные фиксируются в диагностической карте и применяются для коррекции методов образования, подбора новых технологий и закрепления знаний.

В процессе образования каждый педагог непременно должен проводить диагностику, что позволит получить информацию о правильности выбранного направления развития.

В противном случае обучение не может быть достаточно эффективным, целенаправленным и соответствующим всех необходимым требованиям.

Источник: http://deti.center/doshkolnyy_vozrast/diagnostika_matematicheskogo_razvitiya_detej_doshkolnogo_vozrasta.html

Методики математического развития дошкольников: Игры, Советы

Заботливые родители, как правило, заблаговременно беспокоятся о том, чтобы их чадо получило необходимые знания в преддверии школы. От того, как будут выстроены занятия, и какие знания получит ребенок, напрямую зависит его школьная успеваемость и мотивация на учебу в дальнейшем. Что необходимо учитывать, организуя занятия с ребенком?

Советы по организации занятий для ребенка

1. Выстраивайте занятия в игровой форме. Для дошкольника это лучшая форма усвоения нового материала. Если вы просто посадите малыша за стол и объявите, что «сейчас будем заниматься», он может заскучать, впоследствии начать отказываться от столь обременительных «уроков».
2. Занимайтесь только тогда, когда ребенок находится в хорошем настроении. Попытка заставить его заниматься тогда, когда ему этого явно не хочется, может привести к рассеянности, плохой концентрации внимания и потере интереса. У ребенка пяти – шести лет преобладает непроизвольная память, поэтому лучше и легче запоминается то, что понравилось, вызвало положительные чувства.
3. Если у ребенка что – то не получается или он не понимает задачу, нужно терпеливо объяснять ему несколько раз до тех пор, пока ему не станет все предельно ясно. Любые требования и негативные оценки способны навсегда отбить у ребенка желание заниматься.
4. Занимайтесь систематически, регулярно внося что – то новое в процесс обучения. Дело в том, что ребенку очень быстро приедается однообразие. А если потерян интерес, информация не будет восприниматься на должном уровне. Занятия должны быть регулярными, чтобы ребенок постоянно актуализировал свои знания, тренировал навыки и умения.

Методики математического развития дошкольников

Ниже приведены упражнения, помогающие развить у ребенка математические способности и подготовиться к обучению в школе. В идеале к моменту поступления в первый класс ваши сын или дочка должны уметь считать от одного до двадцати, знать цифры, уметь их сопоставлять (какая цифра больше или меньше).

«Разложи по порядку»

Для выполнения этого упражнения вам понадобятся карточки с четким изображением цифр. Ребенок должен знать числовые значения и уметь ориентироваться в понятиях «больше — меньше».

Даем ребенку задание: разложи карточки по порядку, начиная от самой маленькой цифры и заканчивая самой большой.

Упражнение прекрасно тренирует память, развивает воображение, способствует закреплению пройденного материала.

«Сосчитай предметы»

Для выполнения этого упражнения вам понадобятся карточки с любыми предметами или изображениями животных. На карточке также должны быть написаны цифры. Задача ребенка заключается в том, чтобы сосчитать количество предметов на карточке и обвести карандашом то числовое значение, которое соответствует количеству расположенных предметов. Как правило, с этим особенных трудностей не возникает.

«Сравнение и анализ чисел»

Для выполнения этого упражнения вам понадобятся карточки с изображениями цифр. Вы показываете ребенку две карточки и предлагаете их сравнить. Например: вот карточки с числами. Назови их, пожалуйста.

Таким образом,  развитие у ребенка математических способностей полностью находится в руках родителей. Крайне важно подойти к процессу обучения со всей ответственностью, тогда и положительные результаты не заставят себя долго ждать.

• Полезные статьи:
• БЫСТРЫЙ СПОСОБ ВЫУЧИТЬ ТАБЛИЦУ УМНОЖЕНИЯ
• ИГРЫ ДЛЯ ОБУЧЕНИЯ СЧЕТУ
• ЗАНЯТИЯ ПО КУБИКАМ ЗАЙЦЕВА

Источник: http://razvitiedetei.info/doshkolnoe-razvitie/metodiki-matematicheskogo-razvitiya-doshkolnikov.html

Значение и задачи математического развития детей дошкольного возраста

Проблема обучения математике в современной жизни приобретает все большее значение. Это объясняется, прежде всего, бурным развитием математической науки и проникновением ее в различные области знаний.

Повышение уровня творческой активности, проблемы автоматизации производства, моделирования на электронно-вычислительных машинах и многое другое предполагает наличие у специалистов большинства современных профессий достаточно развитого умения четко и последовательно анализировать изучаемые процессы. Поэтому обучение в детском саду направлено, прежде всего, на воспитание у детей привычки полноценной логической аргументации окружающего. Опыт обучения свидетельствует о том, что развитию логического мышления дошкольников в наибольшей мере способствует изучение начальной математики. Для математического стиля мышления характерны четкость, краткость, расчлененность, точность и логичность мысли, умение пользоваться символикой. В связи с этим систематически перестраивается содержание обучения математике в школе и детском саду.

Естественно, что основой познания является сенсорное развитие, приобретаемое посредством опыта и наблюдений. В процессе чувственного познания формируются представления – образы предметов, их свойств, отношений.

Так, оперируя разнообразными множествами (предметами, игрушками, картинками, геометрическими фигурами), дети учатся устанавливать равенство и неравенство множеств, называть количество словами: «больше», «меньше», «поровну». Сравнение конкретных множеств подготавливает детей к усвоению в последующем понятия числа.

Именно операции с множествами являются той основой, к которой обращаются дети не только в детском саду, но и на протяжении последующих лет обучения в школе. Представление о множестве формирует у детей основы понимания абстрактного числа, закономерностей натурального ряда чисел.

Хотя понятия натурального числа, а также геометрической фигуры, величины, части и целого абстрактны, все-таки они отображают связи и отношения предметов окружающей действительности.

Доказано, что ознакомление детей с разными видами математической деятельности в процессе целенаправленного обучения ориентирует их на понимание связей и отношений.

Под математическим развитием дошкольников, как правило, понимают качественные изменения в формах познавательной активности ребенка, которые происходят в результате формирования элементарных математических представлений и связанных с ними логических операций. Анализ научных исследований (А.М. Леушина, Н.И. Непомнящая, А.А. Столяр и др.

), педагогического опыта убеждает в том, что рационально организованное обучение дошкольников математике обеспечивает общее умственное развитие детей. (Рационально организованное – это своевременное, соответствующее возрасту и интересам детей обучение.) При этом важное значение имеет педагогическое руководство со стороны взрослого (воспитателя или родителей).

Дети приобретают элементарные знания о множестве, числе, величине и форме предметов, учатся ориентироваться во времени и пространстве. Они овладевают счетом и измерениями линейных и объемных объектов с помощью условных и общепринятых мер, устанавливают количественные отношения между величинами, целым и частями.

В математической подготовке детей, развитии элементарных математических представлений важную роль играет обучение измерению как начальному способу познания количественной характеристики окружающего.

Это дает возможность дошкольникам прежде всего пользоваться не общепринятыми, а условными мерами при измерении сыпучих, жидких веществ и протяженностей.

Одновременно у детей развивается глазомер, что весьма важно для их сенсорного развития.

В процессе систематического обучения математике дети овладевают специальной терминологией – названиями чисел, геометрических фигур (круг, квадрат, треугольник, ромб и др.), элементов фигур (сторона, вершина, основание) и т. п.

Однако не рекомендуется в работе с детьми использовать такие слова-термины, как «натуральный рад», «совокупность», «структура», «элементы множества» и др. При этом работа не ограничивается только занятиями.

Занятия по математике приобретают особое значение в связи с развитием у детей познавательных интересов, умений проявлять волевые усилия в процессе решения математических задач.

Как правило, учебные задачи на занятиях решаются в сочетании с воспитательными. Так, воспитатель учит детей быть организованными, самостоятельными, внимательно слушать, выполнять работу качественно и в срок.

Это дисциплинирует детей, способствует формированию у них целенаправленности, организованности, ответственности. Таким образом, обучение детей математике с раннего возраста обеспечивает их всестороннее развитие.

Среди задач по формированию элементарных математических знаний и последующего математического развития детей следует выделить главные, а именно:

• приобретение знаний о множестве, числе, величине, форме, пространстве и времени как основах математического развития;
• формирование широкой начальной ориентации в количественных, пространственных и временных отношениях окружающей действительности;
• формирование навыков и умений в счете, вычислениях, измерении, моделировании, общеучебных умений;
• овладение математической терминологией;
• развитие познавательных интересов и способностей, логического мышления, общее интеллектуальное развитие ребенка.

Эти задачи чаще всего решаются воспитателем одновременно на каждом занятии по математике, а также в процессе организации разных видов самостоятельной детской деятельности.

Многочисленные психолого-педагогические исследования и передовой педагогический опыт работы в дошкольных учреждениях показывают, что только правильно организованная детская деятельность и систематическое обучение обеспечивают своевременное математическое развитие дошкольника.

Многочисленными исследованиями (А.М. Леушина, Н.А. Менчинская, Г.С. Костюк и др.) доказано, что возрастные возможности детей дошкольного возраста позволяют формировать у них научные, хотя и элементарные, начальные математические знания.

В связи с этим на конкретных возрастных этапах создаются наиболее благоприятные условия формирования определенных знаний и умений.

Так, во второй младшей группе детского сада (четвертый год жизни) основное внимание уделяется формированию знаний о множестве. Понятие о множестве является одним из основных и наиболее общих, оно проходит через всю математику. Понятие множества настолько широко, что не определяется даже на современном уровне развития науки, а вводится как изначальное и поясняется на конкретных примерах.

В средней группе в процессе изучения основных свойств множества формируется понятие о числе, а в старшей – первые представления о натуральном ряде чисел. В дошкольном возрасте понимание основных свойств множества ограничено.

Однако осознание отдельных его свойств (равенство и неравенство, независимость мощности множества от качественных его признаков) возможно уже в младшем дошкольном возрасте.

Наряду с формированием начальных математических представлений и понятий программа воспитания в детском саду предусматривает ознакомление детей дошкольного возраста с рядом математических зависимостей и отношений.

Так, дети осознают некоторые отношения между множествами (равномощность – неравномощность; отношения порядка в ряду величин, натуральных чисел; пространственные и временные отношения и т.д.). При этом все математические знания подаются во взаимосвязи.

Например, формирование представлений о количестве связано с формированием представлений о множестве и величине предметов с развитием умений видеть, условно определять размер, параметры, а также с усвоением отношений между предметами.

Формирование начальных математических знаний во взаимосвязи позволяет постепенно и целенаправленно конкретизировать и уточнять каждое из выделенных свойств.

Ознакомление детей с мерой и измерениями способствует формированию более точного понимания числа, и прежде всего единицы.

Именно связь счета и измерения помогает ребенку осознать зависимость результата счета (измерения) от единицы счета (условной меры).

На занятиях по математике в детском саду формируются простейшие виды практической и умственной деятельности детей.

Под видами деятельности – в этом случае способами обследования, счета, измерения – понимают объективные последовательные действия, которые должен выполнять ребенок для усвоения знаний: поэлементное сравнение двух множеств, накладывание меры и др.

Овладевая этими действиями, ребенок усваивает цель и способы деятельности, а также правила, обеспечивающие формирование знаний. Например, сравнивая равные и неравные между собою множества, накладывая или прикладывая элементы, ребенок осознает понятие количества. Поэтому особое внимание уделяется развитию практических действий детей с предметами.

Центральной задачей математического развития детей в детском саду является обучение счету. Основными способами при этом являются накладывание и прикладывание, овладение которыми предвосхищает обучение счету с помощью слов-числительных.

), строить ряды предметов по их размеру в порядке возрастания или уменьшения (большой, маленький, еще меньше, самый маленький).

Однако, для того чтобы ребенок усвоил эти понятая, необходимо сформировать у него конкретные представления, научить его сравнивать предметы между собой сначала непосредственно – накладыванием, а потом опосредованно – с помощью измерения.

Программа по математике в детском саду предусматривает развитие глазомера детей при определении размера предметов. Для этого их обучают оценивать размер (величину предметов) в целом или по отдельным параметрам, сопоставляя с размером известных предметов.

Обращается внимание на формирование умения проверять правильность оценки в своей практической деятельности, используя добавления, уменьшения и др. Каждое практическое действие пополняет знание детей новым содержанием.

Доказано, что формирование элементарных математических знаний происходит одновременно с выработкой у них практических умений и навыков

Практические действия, выполняя определенную роль в математическом развитии детей, сами не остаются неизменными. Так, осуществляется изменение деятельности, связанной со счетом.

Сначала она опирается на практическое поэлементное сравнение двух конкретных множеств, а позднее особое значение приобретает число как показатель мощности множества и натуральный ряд чисел, что впоследствии заменяет одно из конкретных множеств.

Сначала дети берут предметы руками, перекладывают их, а потом считают предметы, не дотрагиваясь до них, или воспринимают только на ощупь.

Уровень овладения детьми умственными операциями зависит от использования специальных методических приемов, которые позволяют детям упражняться в сравнении, обобщении. Так, дети учатся сравнивать множества по количеству, осуществляя при этом структурный и количественный анализ множества.

Сравнивая предметы по форме, дети выделяют размер отдельных элементов, сопоставляя их между собою.

Важной является задача развития у детей мышления и речи (овладение математической терминологией).

Следует значительно больше внимания уделить развитию начальных умений индуктивного и дедуктивного мышления, формированию у детей познавательных интересов и способностей.

Следует отметить, что общие методы познания составляют основу любого научного мышления, в том числе и математического. Естественно, последнее имеет свое особое значение.

На практике нередко наблюдается одностороннее понимание способностей как узкоспециальных, что граничат с одаренностью. В связи с этим воспитатели иногда недооценивают формирование у всех детей общих познавательных способностей.

Любая деятельность невозможна, если человек не имеет к ней способностей. В психологии способности обозначаются как качества личности, необходимые для успешного выполнения деятельности.

Способности следует рассматривать не только в связи с определенным видом детской деятельности, но и в связи с ее общей структурой, в которой прежде всего выделяются ориентировочные и исполнительские действия.

И когда мы говорим об общих способностях к деятельности, то имеем в виду, насколько ребенок в состоянии использовать свои знания, умения, навыки, каков у него уровень познавательной самостоятельности. Все это определяет эффективность исполнительской части общих способностей.

Наряду с этим следует формировать у детей умения абстрагировать, выделять главное.

Итак, математическое развитие детей предполагает широкую программу приобщения их к деятельности, в данном случае математической, которой руководит взрослый (воспитатель, родители).

В процессе систематического обучения математике дети овладевают специальной терминологией: названием чисел, … фигур, элементов фигур (сторона, …), математических действий (сложение,…) и др. Основными задачами математического развития детей являются:

1. накопление дошкольниками знаний о множестве, величине, пространстве и…;
2. формирование начальной ориентации в количественных, …и временных отношениях;
3. формирование умений и навыков в счете, … и др;
4. овладение детьми… терминологией;
5. развитие у них … интересов и умственное развитие ребенка в целом.

Похожие материалы в разделе Психология ребенка:

Источник: https://Psylist.net/pedagog/00302.htm